Wikipedia & Benford's Law
Benford’s law is the tendency for small digits to be more common than large ones when looking at the first non-zero digits in a large, heterogenous collection of numbers. These frequencies range from about 30% for a leading 1 down to about 4.6% for a leading 9, as opposed to the constant 11.1% you would get if they all appeared at the same rate.
Since I recently wrote about unpacking the pages from a dump of the English Wikipedia, I thought would see if Benford’s law manifested in the text of Wikipedia, as it seems like it fits the idea of a “large, heterogenous collection of numbers” quite well.
The notebook containing the full code is here.
Description of Benford’s Law
A set of numbers is said to follow Benford’s law if the frequencies leading digits \(d \in {1,…,9}\) follow the probability distribution
$$ P(d) = \log_{10} \left(1 + \frac{1}{d}\right) $$
Explanations for exactly why this works are beyond the scope of the article; the Wikipedia page tries to offer some insight into nature of the law, though. So the actual probabilities of each digit are
| Digit | Probability |
|---|---|
| 1 | 0.301 |
| 2 | 0.176 |
| 3 | 0.125 |
| 4 | 0.097 |
| 5 | 0.079 |
| 6 | 0.067 |
| 7 | 0.058 |
| 8 | 0.051 |
| 9 | 0.046 |
So a 1 or a 2 would be the first digit nearly half the time, while an 8 or a 9 would lead less than a tenth of the time between them.
This phenomenon does appear in a fairly broad range of situations, enough that it can be invoked as a tool for fraud detection, among other things. Frank Benford, the law’s namesake, published a paper on this titled “The Law of Anomalous Numbers” in 1938 (though the idea had been explored before). In it, he goes through several different datasets from fairly diverse sources, like newspaper texts and molecular weights, and finds that there is good agreement with this theory given a few conditions. Probably the most prominent – and most relevant for this data – is whether the data span several orders of magnitude, particularly if the numbers are generated by several different sources. As the abstract of Benford’s paper put it:
An analysis of the numbers from different sources shows that the numbers taken from unrelated subjects, such as a group of newspaper items, show a much better agreement with a logarithmic distribution than do numbers from mathematical tabulations or other formal data. There is here the peculiar fact that numbers that individually are without relationship are, when considered in large groups, in good agreement with a distribution law – hence the name “Anomalous Numbers.”
It seems like this assumption would hold well for Wikipedia data, since you can get information on very unrelated topics like budgetary spending to astronomy to history. In that sense, Wikipedia seems like one of the best possible datasets to apply Benford’s law to.
Checking the Dump: Strategies
I settled on three different strategies to look at the data, based on some testing and experimentation that I did on a dump of the Simple English Wikipedia. It’s a pretty good dataset for working out something for the English Wikipedia, as it has essentially the same challenges for processing the text while being much smaller (a couple hundred megabytes when compressed, versus 17.4 gigabytes for the regular English Wikipedia).
As a first attempt, we can just search for everything that looks like a number – digits, possibly with commas or periods as separators – and extract it from the page text. This can be done with a fairly straightforward regular expression, so it’s quick and easy to implement.
Checking every possible number may not be the best strategy, though. Again from Benford’s paper:
The best agreement was found in the arabic numbers (not spelled out) of consecutive front page news items of a newspaper. Dates were barred as not being variable, and the omission of spelled-out numbers restricted the counted digits to numbers 10 and over.
We don’t have to worry about the number-searching regex finding the spelled-out numbers, but the point about dates is relevant. Having flipped through a lot of Wikipedia articles myself, I know many will have sentences that start with “In November 2017…” or something similar. An excess of those could lead to an excess of numbers starting with 1 or 2, so those should be filtered out. Exactly how to do that is somewhat complicated, though, since there are a lot of contexts where a four-digit year could appear, and accounting for all of them requires either applying NLP to each article (not practical with this much text) or an extensive selection of regular expressions.
So strategy number two was to add a collection of regular expessions to filter out most common date formats, as well as a few obvious contexts for years to appear on their own. I also added some code for removing the contents of some reference and internal file links. In the Simple English Wikipedia, I saw that the reference links in particular often have some kind of ID number starting with a 9 and that didn’t appear in the actual text, so I didn’t want to risk that affecting the distribution.
The experimentation on the Simple English Wikipedia suggested that strategy two improved things, but some significant differences between Benford’s law and what I found remained. So the third strategy was essentially the second, but with some additional regexes to eliminate any four-digit number that looked like it could be a year. This was probably overkill, but again, any code precise enough to identify whether a four-digit number was a year or not would be too unwieldy to be practical on one machine.
Checking the Dump: Code
Information on exactly how to read the dump can be found in the post linked at the start, so I’ll focus on the actual processing code here. The libraries needed are:
import bz2
from collections import Counter
import os # needed in preliminary code for defining bz2 streams; not used in processing
import re
from bs4 import BeautifulSoup
import pandas as pd # only if you're storing results from subsets of articles
from tqdm import tqdm # progress bar only, not functionally necessaryTo start with, there are about 20 million pages in the dump, but the English Wikipedia only has six million and change articles. So filtering those out before we start applying a lot of regular expressions helps a lot.
def get_page_name(page_element):
return page_element.find('title').text
def is_redirect(page):
# determine if a page is a redirect page
return page.find("redirect") is not None
def filter_bad_pages(page_list):
UNUSED_PAGE_PREFIXES = ["User:", "Wikipedia:", "User talk:", "Talk:", "Wikipedia talk:",
"Template:", "Help:", "MediaWiki:", "Help talk:", "MediaWiki talk:",
"File:", "Category:", "Template talk:", "Category talk:", "WT:",
"US:", "CAT:", "T:", "MOS:", "File talk:", "Module:", "H:"]
page_list = [p for p in page_list if not is_redirect(p)]
for prefix in UNUSED_PAGE_PREFIXES:
page_list = [p for p in page_list if not get_page_name(p).startswith(prefix)]
return page_listNext is defining the regular expressions to filter the dates. There’s a lot of them, and they’re all used in the same way – as the first argument to re.sub() – so I’ll just show the regexes themselves, organized by the function that calls them:
# remove_non_text() - internal links with numbers that don't appear in page text
file_link = "\[\[File:.*?\]\]"
image_link = "\[\[Image:.*?\]\]"
ref_link "{{.*?}}"
# remove_dates_and_times()
months = ["January", "February", "March","April", "May", "June", "July", "August", "September",
"October", "November", "December"]
month_day_year_words = f"({'|'.join(months)})" + " ([0-9]{1,2})?(,)? [0-9]{4}"
day_month_year_words = "([0-9]{1,2}) " + f"({'|'.join(months)})" + "(,)? [0-9]{4}"
year_first_numbers = "[0-9]{4}[-/][0-9]{1,2}[-/][0-9]{1,2}"
year_last_numbers = "[0-9]{1,2}[-/][0-9]{1,2}[-/][0-9]{4}"
times = "([0-2]?[0-9]:[0-5][0-9])( AM| PM)?"
month_day_words = f"({'|'.join(months)})" + " [0-9]{1,2}"
day_month_words = "[0-9]{1,2} " + f"({'|'.join(months)})"
# remove_lone_years()
in_year = "[Ii]n [12][0-9]{3}"
year_range = "[12][0-9]{3}(-| to )[12][0-9]{3}"
from_year = "[Ff]rom [12][0-9]{3}"
year_in_parentheses = "\([12][0-9]{3}\)"
# remove_all_years()
second_millenium_years = "1[0-9]{3}"
third_millenium_years = "20[0-9][0-9]"After using whichever regular expressions you want for filtering the text, you apply one last regex for finding the numbers and then get the first digit:
def get_first_digits_from_page(page_text):
numbers = re.findall("[0-9.,]{1,}", page_text)
numbers = [n.lstrip("0.,")[0] for n in numbers if re.search("[1-9]", n)]
return Counter(numbers)str.lstrip() is pretty convenient here since we want the first digit from 1 to 9 that appears, but the regex “[0-9.,]{1,}” will catch decimals like 0.002 as well. Also note the fact that we’re returning this as a Counter object – it has a defined addition operation that totals up the counts for items that appear in both objects, which makes it very easy to combine the counts from multiple pages.
Finally, the main loop. It first extracts a single section (“stream”) from the bz2 file containing the Wikipedia pages, using a list of the start bytes for each stream. It then, decompresses the stream and searches the pages for all of the numbers using the three strategies discussed earlier. After every 100 streams, it takes the total counts for all three strategies, adds it to a pandas dataframe as a new row (I set that up so I wouldn’t lose results if I had to cancel it mid-run), and then resets the count.
def get_page_text(page_element):
revision = page_element.find('revision')
return revision.find('text').text
benford1 = Counter({str(i):0 for i in range(1,10)})
benford2 = Counter({str(i):0 for i in range(1,10)})
benford3 = Counter({str(i):0 for i in range(1,10)})
benford_df = pd.DataFrame()
stream_file = open(DUMP_FILE, "rb")
for i in tqdm(range(len(start_bytes)-1)):
# isolate and decompress a stream
decomp = bz2.BZ2Decompressor() #bz2 docs say you need a new object for each stream
stream_file.seek(start_bytes[i])
readback = stream_file.read(start_bytes[i+1] - start_bytes[i] - 1)
page_xml = decomp.decompress(readback).decode()
# process it into and as XML
soup = BeautifulSoup(page_xml)
page_list = filter_bad_pages(soup.find_all("page"))
page_texts = [get_page_text(p) for p in page_list]
for pt in page_texts:
# had some pages in the Simple English wiki that wouldn't process, kept this for safety
try:
# strategy 1 - all numbers
count1 = get_first_digits_from_page(pt)
# strategy 2 - strip dates, times, and links
pt = remove_non_text(pt)
pt = remove_dates_and_times(pt)
pt_no_lone_years = remove_lone_years(pt)
count2 = get_first_digits_from_page(pt_no_lone_years)
# strategy 3 - remove anything like a year
pt = remove_all_years(pt)
count3 = get_first_digits_from_page(pt)
benford1 = benford1 + count1
benford2 = benford2 + count2
benford3 = benford3 + count3
except:
pass
# every 100 streams, store counts and reset the objects
if (i+1) % 100 == 0:
new_row = {}
for i, b in enumerate([benford1, benford2, benford3]):
for k in b.keys():
new_row[f"{i}_{k}"] = b[k]
benford_df = benford_df.append(new_row, ignore_index=True)
benford1 = Counter({str(i):0 for i in range(1,10)})
benford2 = Counter({str(i):0 for i in range(1,10)})
benford3 = Counter({str(i):0 for i in range(1,10)})
stream_file.close()
# final round for any remaining streams
new_row = {}
for i, b in enumerate([benford1, benford2, benford3]):
for k in b.keys():
new_row[f"{i}_{k}"] = b[k]
benford_df = benford_df.append(new_row, ignore_index=True)I presented the strategies as being separate, but I ran all three at the same time for efficiency reasons – since the strategies built on each other, it’s fairly easy to execute all three in one run. Even then, it still took over nine hours to complete on my machine (timed with the progress bar from tqdm), so doing it this way undoubtedly saved many hours.
Results
The first strategy – grab all of the numbers – ended up collecting about 803,000,000 numbers in the text. Since all of the years are left in, thise does end up with much more weight on 1 and 2 than Benford’s law would predict (blue bars are the measured frequencies, the black line is the theoretical frequencies):
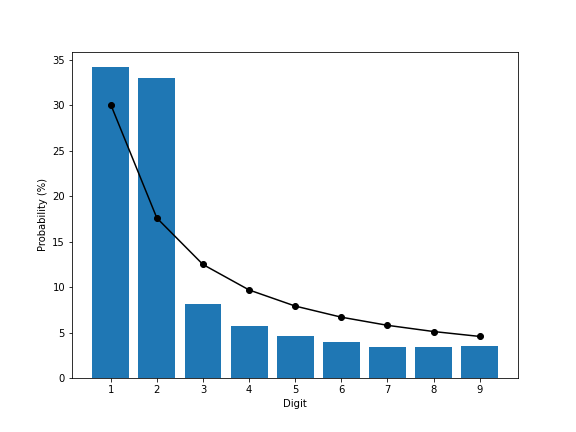
Numbers starting with 2 are more common than in Benford’s law by 15 percentage points, which is pretty drastic. I’m a little surprised that numbers starting with 1 aren’t similarly more common – I would have guessed that there would be enough mentions of years starting with 1 to push that count up to at least 40% of all of the numbers. Regardless, it means that 3 through 9 are much less frequent that expected.
Strategy two dealt with filtering out obvious years. This had a big impact on the count of the numbers found, dropping it to about 406,000,000 numbers, but the effect on the distribution is less pronounced:
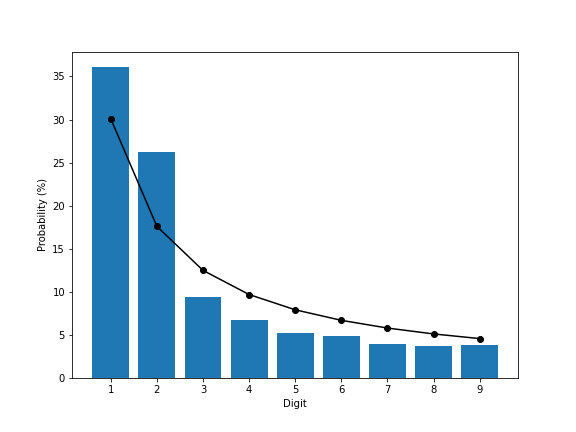
I had expected this to decrease the counts of 1s and 2s significantly, particularly the 2s given how common they were with the first strategy. Instead, the 2s drop somewhat but are still excessively common, and all others, including the 1s, rise between 0.3 and 2 percentage points. It’s closer than before, but still not a great match.
The third strategy was to strip out anything that was probably a four-digit year. This had a smaller effect on the absolute count, only reducing it to 325,000,000, but it does have a more pronounced effect on the distribution:
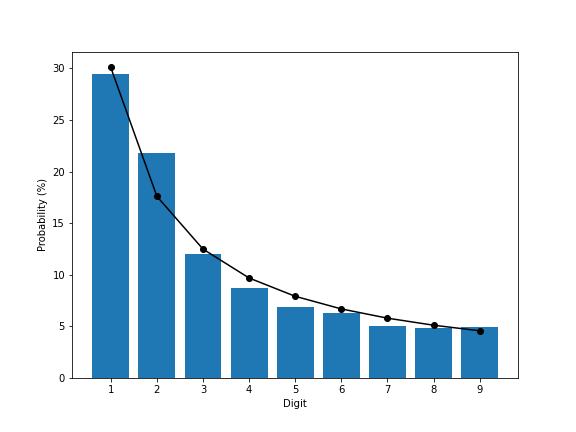
The 1s and 2s combined lose a share of about 11%. The 2s are still about 4 percentage points above Benford’s law, but all other values are off by about 1 percentage point or less.
The actual frequencies that I found (in percentages):
| Digit | Theoretical | Strategy 1 | Strategy 2 | Strategy 3 |
|---|---|---|---|---|
| 1 | 30.10 | 34.19 | 36.06 | 29.48 |
| 2 | 17.61 | 32.97 | 26.20 | 21.85 |
| 3 | 12.49 | 8.17 | 9.43 | 12.04 |
| 4 | 9.69 | 5.68 | 6.76 | 8.70 |
| 5 | 7.92 | 4.65 | 5.27 | 6.83 |
| 6 | 6.69 | 3.98 | 4.86 | 6.27 |
| 7 | 5.80 | 3.41 | 3.90 | 5.06 |
| 8 | 5.12 | 3.46 | 3.74 | 4.86 |
| 9 | 4.58 | 3.49 | 3.77 | 4.91 |
Conclusions
So the third strategy produced the closest proportions to Benford’s law, which means that Wikipedia could be obeying Benford’s law fairly well. That it’s the third strategy makes sense given the comments in Benford’s paper when he tried to analyze newspaper text, since Wikipedia has historical info on a lot of topics and dates will pop up a lot as a result. I don’t understand where the excess numbers of 2s are coming from, though – it’s interesting that even the third strategy still saw a notable excess, which suggests something else may be going on here.